Overview of ANOVA

Overview

GeneLinker™ provides two different methods for performing a one-way Analysis of Variance, or ANOVA: The F-Test and the Kruskal-Wallis test. These methods are used to determine which genes vary most significantly between a set of conditions. If one has replicate chips measuring, for example, subjects treated with a drug and treated with a placebo, ANOVA can be used to rank the genes according to their change between the treatment and control conditions. ANOVA can be used to compare several conditions simultaneously, not just two at a time. ANOVA is most effective when all groups are the same size, each containing at least three samples (replicates).

When you carry out an ANOVA GeneLinker™ calculates a p-value for each gene. The p-value is the probability that the variation between conditions may have occurred by chance, so genes with smaller p-values are varying more significantly. The gene’s variation is less likely to have occurred by chance, and is conversely more likely to be connected to the difference in conditions. When you view an ANOVA result in GeneLinker™, the most significantly-varying genes – those with the smallest p-values – appear at the top of the list.

The conditions are specified by importing a variable, called the Grouping Variable. The different values of the Grouping Variable represent the different conditions between which significant variation may take place. For example if the Grouping Variable chosen looks like this:

then the first three samples will be considered replicates under one condition (A), and the second three samples will be considered replicates under another condition (B). The ANOVA will determine whether the variation between group A and group B is significantly greater than the (presumably random) variation within each group.

Note: If you do not have any replicates in your data, GeneLinker™ will display 'Undefined' for the p-value of every gene. 'Undefined' can also be computed for individual genes in certain circumstances, e.g. if there is no variation in the expression level of the gene.

A common use of the ANOVA is to remove invariant genes from a dataset. To do this:

1. Carry out an ANOVA.

2. Select the most significant genes in the ANOVA viewer. You may either choose a threshold p-value or choose some number of genes that is useful to you.

3. Create and save a gene list from this selection.

4. Use Gene List Filtering to generate a new data table containing only those genes which vary significantly.

See ANOVA Viewer for instructions on creating a gene list from ANOVA results.

Choosing between the F-Test and Kruskal-Wallis

The F-Test is a parametric test which is based on certain assumptions of normality about the data. The Kruskal-Wallis Test is a non-parametric test which makes no such assumptions. Because the Kruskal-Wallis Test uses only the rankings of the data points and not their absolute values, it is a less powerful test than the F-Test and may underestimate the significance of the changes in some genes (ie. compute too large a p-value). If your data is approximately normal, or can be transformed so that it is, you should use the F-Test. If not, then use the Kruskal-Wallis Test.

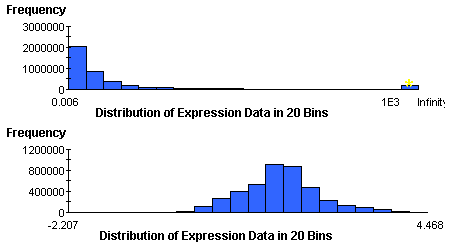
Gene expression abundances are rarely normal, but are frequently log-normal. You can estimate the normality of your data visually using the Summary Statistics Chart in GeneLinker™. If the data is strongly skewed to the left, as in the first picture below, then you should first transform it using a Logarithm normalization. Viewing the Summary Statistics on the log-normalized data table should produce a normal histogram much like the one in the second picture. The second data table is suitable for application of the F-Test.

P-values and multiple testing

The p-value computed by GeneLinker™ is to be interpreted for each gene as the probability that the variation in that gene is random. When the test is being applied to thousands of genes – as is usually the case in microarray experiments – then even purely random data will contain some genes with small (significant) p-values. For example, if you choose to consider for further experimentation any gene with a p-value of less than 5% or 0.0500, then you can reasonably expect that about 5% of those genes are false positives, or genes which have obtained a small p-value by random chance. If you are using ANOVA as a gene filter and it is important to you to minimize the number of false positives, then you should choose a smaller p-value as a cutoff. For instance, if you are testing 1000 genes and want only a 50% chance of having one false positive in your gene list, then you should select only genes with p < 0.50/1000, or 0.0005. Be warned, however, that you will also be discarding genes which have real differential expression by so doing, ie. you will increase the number of false negatives as you decrease the number of false positives. The systematically varying genes and the randomly varying genes will be intermixed in any real dataset. The only way to separate them better – the only way to decrease both the false positive rate and the false negative rate – is to do more experiments and obtain more replicates.

The simple adjustment of the p-value described above is technically known as a Bonferroni correction. The Bonferroni correction is rather conservative (ie. severe) but has the virtue of simplicity. For more discussion of multiple testing corrections to microarray data, see for example S. Dudoit, Y. H. Yang, M. J. Callow and T. P. Speed, "Statistical methods for identifying differentially expressed genes in replicated cDNA microarray experiments" (2000), Stanford University Technical Report #578.

F-Test Algorithm

For a gene with M groups of samples, where each group I has Ni replicates (I = 1,2,...M) we want to determine if the gene has significantly changed between any pair of groups. The F-statistic is the ratio of two variances:

F = var_1/var_2

The null hypothesis is that the two variances are the same. The statistic follows a distribution parameterized by nu_1 = n1 – 1 and nu_2 = n2 – 1, where n1 and n2 are the number of samples in the populations used to calculate var_1 and var_2.

To use the F-test to filter genes, the F-statistic is first determined by calculating the total variations between and within samples. The result can be proven to follow the F-distribution.

variation_between_samples = [S[i=1..M] S[j=1..Ni](Yi – Y)2], n1 = M -1

variation_within_samples = [S[i=1..M](S[j=1..Ni](Yij – Yi)2)], n2 = (S[i=1..M]Ni)-M

The relevant F-statistic is then formed by taking:

F = (variation_between_samples/n1)/(variation_within_samples/n2)

The probability of this F-value arising from two identical distributions gives us a measure of the significance of the between-sample variation as compared to the within-sample variation. Small p-values indicate a low probability of the between-sample variation being due to sampling of the within-sample distribution, so small p-values indicate interesting genes.

Kruskal-Wallis Algorithm

The Kruskal-Wallis algorithm is analogous to the F-Test, except that instead of operating on the expression values directly it operates on the ranks of the expression values. That is, each gene first has its expression values sorted and a rank assigned to each value based on its position in the sorted list. The variances of the rank numbers within each group are computed, and the test proceeds as the F-Test described above.